HOME - INTRODUZIONE - PERSONAGGI PRINCIPALI - PROBLEMI FAMOSI
I tre problemi più famosi che i greci hanno risolto sono:
|
I greci, pur essendo riusciti a risolvere questi problemi, non furono soddisfatti del loro lavoro. Infatti volevano risolverli usando solamente una riga non graduata e un compasso, mentre ci riuscirono solo usando semplici linee curve.
Questi
studi comunque li condussero alla scoperta di molte altre nozioni matematiche.
La
dimostrazione di queste soluzioni non viene proposta per la complessità degli
argomenti.
Ippocrate
nacque probabilmente nel 460 a.c. e morì nel 380 a.c. Esercitò come prima
attività quella del mercante poi, in seguito al trasferimento ad Atene nel 430,
si dedicò allo studio della geometria e divenne famoso per importanti
contributi, tra i quali la quadratura delle lunule e la produzione del primo
libro riguardante la geometria.
Ippocrate inoltre costituì una propria raccolta che anticipò di un secolo gli elementi presi in considerazione da Euclide. Questo manuale venne perduto, nonostante fosse conosciuto da Aristotele. Ippocrate scrisse in questo testo il problema sulla quadratura delle lunule che deriva dalla quadratura del cerchio.
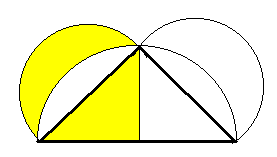
Le lunule sono regioni piane
delimitate da archi appartenenti a due differenti circonferenze.
Ippocrate
probabilmente pensava che la quadratura delle lunule avrebbe portato alla
soluzione del problema alla quadratura dello stesso cerchio.
Ippocrate dapprima ha dimostrato
che, in un triangolo rettangolo con dei semicerchi sui cateti e inscritto in un
altro semicerchio, le lunule formate dal semicerchio che inscrive il triangolo e
da quelli costruiti sui cateti hanno area uguale e che, quindi, ognuna risulta
di area uguale a quella di un triangolo che sia la metà di quello dato. Visto
che ogni triangolo può essere “quadrato”, anche queste lunule possono
essere “quadrate”.
Ippocrate
proseguì prendendo in considerazione un trapezio inscritto in una
semicirconferenza in modo tale che la base minore e i lati obliqui siano
congruenti. Inoltre considerò anche un’altra semicirconferenza il cui
diametro è congruente ai tre lati uguali del trapezio.
Cominciò
dimostrando che l’area dei semicerchi costruiti sui lati congruenti e
dell’altra semicirconferenza sono uguali all’area del semicerchio che
inscrive il trapezio.
Successivamente
dimostrò che i segmenti circolari costruiti sui tre lati congruenti sono
congruenti tra di loro.
Quindi le
lunule che si sono formate più la semicirconferenza a parte sono uguali all’
area del trapezio.
Tuttavia
non riuscì a quadrare una delle lunule che avrebbe portato alla quadratura del
cerchio completo perché erano lunule di tipo diverso da quelle precedenti.
Per questo
Ippocrate non riuscì a risolvere il problema della quadratura del cerchio.
Questo è
uno tra i più celebri problemi non risolti della matematica. Sono state date
numerosi soluzioni ma alcune di queste del tutto ridicole.
Il problema
è il seguente:
costruire un quadrato di area equivalente a un cerchio dato con l’aiuto di riga e compasso.
Il problema
sembra all’apparenza semplicissimo. Questo problema fa parte con la trisezione
dell’angolo e la duplicazione del cubo dei tre problemi classici risalenti
all’antica Grecia. Nessuno riuscì a costruire questo quadrato pur
conoscendone benissimo l’esistenza.
Ora si sa
che il problema è impossibile da risolvere, almeno con riga e compasso.
Se si
considera un cerchio di raggio r, quindi con area r2∏. Quindi
il lato del raggio dipende da r e ∏.
∏ è
un numero particolarissimo poiché è irrazionale e non è il risultato di
nessuna equazione algebrica per cui è impossibile disegnare un quadrato di tali
dimensioni. Pertanto le dimensioni del quadrato sono approssimate e non si
possono rappresentare solamente con riga e compasso.
Per
dimostrare l’impossibilità della quadratura del cerchio si dovette attendere
il 1882 quando F. Lindemann dimostrò la trascendenza di ∏, ovvero che
tale numero non è soluzione di una equazione algebrica a coefficienti
razionali.
Il problema
della trisezione dell'angolo, come è noto consiste, dato un angolo nel
costruirne un altro che sia la terza parte di quello dato.
I
greci, partendo da misure di angoli assegnati, tentarono di costruirne altri che
fossero stati la terza parte.
Questo
procedimento era impossibile facendo uso solo della riga e del compasso.
Ippia è
vissuto nel V secolo a.C. e per
risolvere il problema della trisezione dell'angolo ideò la curva che porta il
suo nome e che viene così costruita:
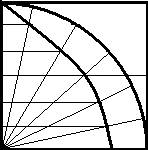
nel
quadrato ABCD si trasli uniformemente la retta AC verso la retta CD,
contemporaneamente si faccia ruotare la retta AD intorno a D in modo che quando
AD coincide con DC, pure AD coincida con DC.
I punti
della curva sono i punti di intersezione delle due rette citate.
Questo
problema, non può essere risolto in modo classico cioè con riga e compasso,
come cercavano di fare gli antichi, tuttavia è possibile risolverlo facendo uso
di altre curve, come questa curva di Ippia.
Con questo
metodo non è solo possibile dividere l'angolo in tre parti ma in un numero
qualsiasi di parti uguali
Secondo una
leggenda,il re Minosse aveva costruito una tomba di forma cubica per il figlio
Glauco, ma quando venne a sapere che essa misurava solo 100 piedi in ciascuna
direzione, pensò che era troppo piccola.
Egli disse
“deve essere raddoppiata nella sua dimensione (in volume)” ed ordinò ai
costruttori di obbedire in fretta al suo ordine raddoppiando i lati della tomba.
I
matematici si resero conto che era stato commesso un errore, poiché in quel
modo la tomba sarebbe diventata otto volte maggiore in volume rispetto a quella
progettata.
Si misero
allora alla ricerca del procedimento per ottenere un volume doppio, ma questo
problema si rivelò tutt’atro che semplice.
Questo
problema venne ricondotto da Ippocrate al problema della costruzione di
due segmenti rettilinei. La scoperta di Ippocrate, tuttavia non risolse il
problema della duplicazione del cubo.
Essa serve
unicamente per trasformare il problema originale in uno di differente enunciato
ma di uguale difficoltà.
In effetti,
nel cercare di risolvere questo problema i greci fecero ricorso all’uso di
altre curve o di altri strumenti diversi dalla riga e dal compasso, trovando
diverse soluzioni del problema, la più famosa è la seguente: la
soluzione di Menecmo.
Si ritiene
che Menecmo abbia scoperto la parabola e l’iperbole equilatera e che ne fece
uso nella soluzione del problema della duplicazione del cubo.